<목차>
1. 정사영(Projection)
2. 내적(Inner Product)
3. 단위벡터(Unit Vector)
4. 사영벡터(Projection Vector)
1.정사영(Projection)
한자뜻을 풀이하자면,
정(正 바를 정) 사(射 쏠 사) 영(影 그림자 영)
= 곧게 쏜 그림자
= 평면과 수직인 빛을 쏘았을 때 생기는 그림자 모양
= 어떤 평면 α 위에 있지 않은 점 A에 대해,
점 A에서 평면 α 위로 내린 수선의 발을 점 A의 평면 α 로의 정사영이라고 한다.

벡터의 정사영도 이와 비슷하다.

2.내적(Inner Product)
쉽게 말하자면, 두 벡터(vector)가 닮은 정도를 나타낸다.
한 벡터가 다른 벡터 방향으로의 성분을 얼마나 가지고 있는지를
두 벡터를 "내적"함으로써 알 수 있다.

한자뜻을 풀이하자면,
내(內안 내) 적(積쌓을 적 = 곱한다) = 벡터를 마치 수처럼 곱하는 개념
벡터에는 방향이 있으므로, 방향이 일치하는 만큼만 곱한다.
E.g. 두 벡터의 방향이 같으면 --> 내적의 값 = 두 벡터 크기의 곱셈
두 벡터가 이루는 각 = 90º --> 일치하는 정도가 없기에 --> 내적의 값 = 0
방향이 일치하지 않을때, 내적의 값을 구하기 위해
한 벡터를 다른 벡터로 정사영 시켜서, 그 벡터의 크기를 곱한다.
벡터의 내적의 결과값은 벡터가 아닌, 스칼라(상수)라는 점!

내적의 기호는 가운데 점을 찍는 것(·)이며,
벡터의 크기를 절대값으로 표시하면, 내적의 값은 다음과 같다.


정확히 말하자면, Inner Product이 Dot Product보다 더 큰 개념이지만,
Dot Product을 내적으로 표현하기도 한다.

Dot Product = Scarlet Product ⊂ Inner Product
예시(1)
Dot Product 예시를 살펴보면,
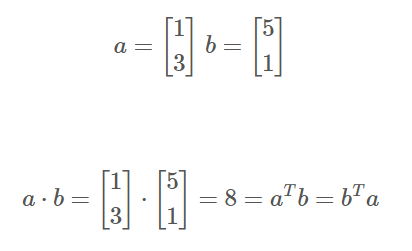
a 와 b의 내적은 각각의 벡터 성분을 곱한 후, 더한 값으로 결과값이 나온다.
전치(transpose)를 수행해도 same.
예시(2)

자기자신을 내적하게 되면, cos(0) = 1이기 때문에
벡터 크기에 제곱한 게 결과값이 된다.
3.단위벡터(Unit Vector)
다양한 방향과 크기를 가진 벡터 중 크기가 1인 벡터를 말한다.
크기가 1이 아닌 벡터를 크기가 1인 단위 벡터로 만드는 것을 "정규화(Normalize)"라고 칭한다.


단위벡터의 필요성
크기, 방향을 한눈에 알아보기 쉽다.

벡터 B = (3 , 4)를 "단위벡터"를 활용해 나타내면, 크기(5)와 방향(3/5, 4/5)을 한눈에 알아볼 수 있다.
벡터와 단위벡터의 상관관계 (최대값, 최소값)


구체적으로...
1) 단위벡터(Unit Vector)가 [1,0] 일 때 = x축 방향

2) 단위벡터(Unit Vector)의 방향이 [4,3]와 같을 때 --> Dot product(내적값) = 최대값



3) 단위벡터(Unit Vector)가 [0,1] 일 때 = y축 방향

4) 단위벡터(Unit Vector)와 벡터(Vector) [4,3]의 각도 = 90º --> Dot product(내적값) = 0

4) 단위벡터(Unit Vector)와 벡터(Vector) [4,3]의 각도 = 180º --> Dot product(내적값) = 최소값


성분을 단위벡터로 나타내기

4.사영벡터(Projection Vector)
정사영(Projection) = 평면과 수직인 빛을 쏘았을 때 생기는 그림자 모양
고로 '벡터의 사영 = 사영벡터'는 빨간색 벡터(크기와 방향을 가짐)다.
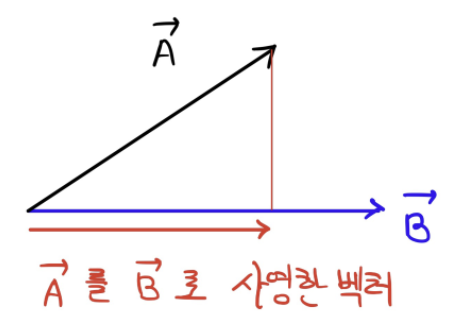
사영벡터 구하는 방법
아래 공식을 살펴보자.

사영벡터(Projection Vector)는 '크기'와 '방향'을 가진 벡터이므로,

예시 1)

벡터 a = [1,3] 를 벡터 b = [5,1]에 정사영(projection)한 사영벡터(projection Vector)값은?

예시 1) 을 기형학적으로 살펴보면...

우선, 사영벡터(Projection Vector)를 미지의 상수(scalar) x̂ 를 활용해 나타내고,

벡터 a 와 벡터 u 뺄셈을 구하면,


※ 개인공부 목적으로 정리한 내용들입니다.
출처
042. 내적 vs 외적
# 내적 | 內積 | inner product **적**은 '쌓는다'는 뜻의 한자이고, 여기서는 '곱한다'는 뜻이다. 벡터의 곱하기는 두 가지 정의가 있는데, 내적은 벡터를 마치…
wikidocs.net
https://m.blog.naver.com/ryumochyee-logarithm/221542210272
벡터의 내적, 정사영으로 깊이 생각하기(개념편)
들어가기... 우리가 고등학교 수학 교과서에서 알 수 있는 정도로만 의미를 파악해 보면 다음과 같이 크게 ...
blog.naver.com
https://sunny-archive.tistory.com/91
내적 (inner product) & 정사영 (projection) 개념으로 Fourier Transform 해석하기
내적, 정사영, 단위벡터 개념을 알아보고 벡터 내적 관점으로 fourier transfrom 식을 해석해봅시다. 내적 (inner product)두 벡터가 얼마나 닮았는가, 즉 닮은 정도를 나타냅니다. 아래의 그림을 보면,
sunny-archive.tistory.com
https://settembre.tistory.com/314
[선형대수] 벡터 Vector
벡터란? 유클리드 공간에서 방향과 크기를 포함하는 기하학적인 대상으로 보통 화살표로 표시한다. 벡터 표현 벡터를 표현할 때 점과 헷갈릴 수 있지만 점과 벡터는 엄현이 다른 것임을 알아야
settembre.tistory.com
https://m.blog.naver.com/seolgoons/221389075503
사영벡터(projection vector)는 뭘까?
안녕하세요, 설군입니다. 사영벡터라는 것에 대해 알아봅시다. 우리는 정사영에 대해 배운적이 있습니다. ...
blog.naver.com
https://www.youtube.com/watch?v=yJSogK2Bmug
https://youtu.be/47axVfuf-Q0?si=eQFRubklJiTPAdmm
'기초 공부 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 5.벡터공간(vector space) 및 부분 공간(sub space) (0) | 2024.09.04 |
|---|---|
| [선형대수학] 4.벡터의 놈(norm) (4) | 2024.09.02 |
| [선형대수학] 2.행렬(Matrix)이란? (0) | 2024.08.31 |
| [선형대수학] 1.선형대수학이란? (1) | 2024.08.31 |
