[선형대수학] 5.벡터공간(vector space) 및 부분 공간(sub space)

<목차>

1. 행렬의 곱셈 4가지 관점

2. 행렬은 선형변환(함수)이다.

3. 벡터공간(vector space)

4. 부분공간(subspace)

5. 행공간(row space)과 열공간(column space)

6. 영공간(null space)

7. 부분 공간(sub space)들간의 관계

1. 행렬의 곱셈 4가지 관점

1) 내적(Inner/Dot product)으로 바라보기

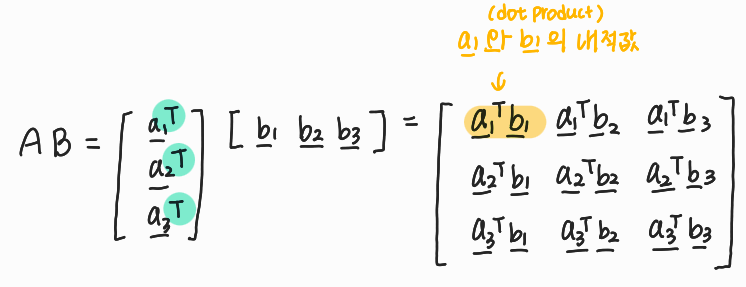
Q.Transpose(T)를 사용한 이유

A. 보통 vector라고 하면, column vector(열) 이기에

    해당 row vector(행)를 나타내기 위해 T를 붙인다.

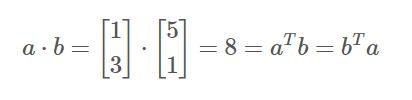
위의 내적값 구하는 공식을 참고하여,

row vector(행) 와 column vector(열)을 곱한 결과값을 보면, 내적값임으로 알 수 있다.

 

2) rank-1 matrix의 합으로 바라보기

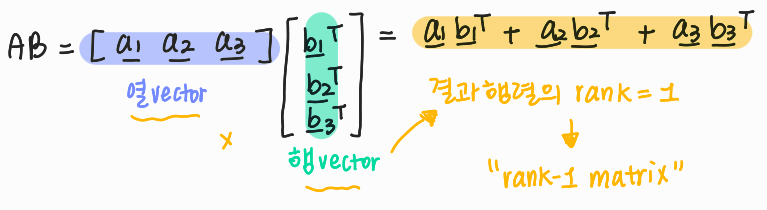
column vector(열)와 row vector(행)을 곱한 결과값을 보면,

결과행렬의 rank =1, 즉 rank-1 matrix의 합임을 알 수 있다.

 

 

3) 열공간(Column Space)으로 바라보기

4) 행공간(Row Space)으로 바라보기

---

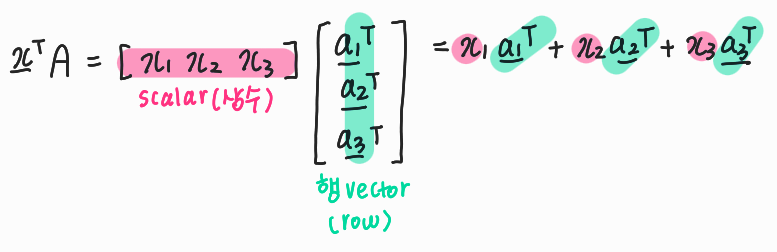
2.행렬은 선형변환(함수)이다. 

선형변환이란?
1) 선형결합을 보존하는,
2) 두 벡터 공간 사이의 함수이다.

 

1) 선형결합을 보존한다.

선형결합을 보존한다는 것은, 해당 2가지 조건을 만족해야한다.

 

2) 두 벡터 공간 사이의 함수이다.

쉽게 말해, 한 점을 한 벡터공간에서 다른 벡터공간으로 이동시키는데 그 이동 규칙을 선형변환이라고 한다.

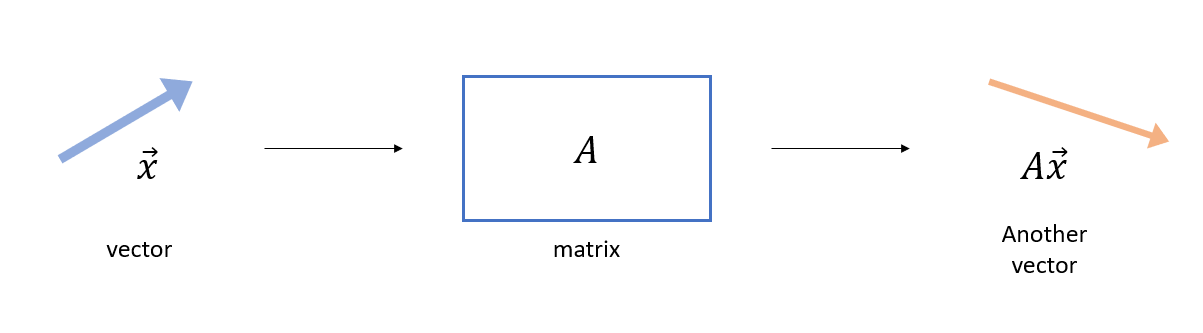
위 그림에서 볼 수 있듯이, 행렬은 벡터를 변환시켜 다른 벡터를 출력해준다.

즉, 행렬은 벡터를 입력받아 벡터를 출력해주는 함수이다.

 

함수란 무엇인가?
함수 f의 정의역 X, 공역 Y, 치역 f(x)일 때,
함수는 정의역의 각 원소를 정확히 하나의 공역 원소에 대응시킨다.

 

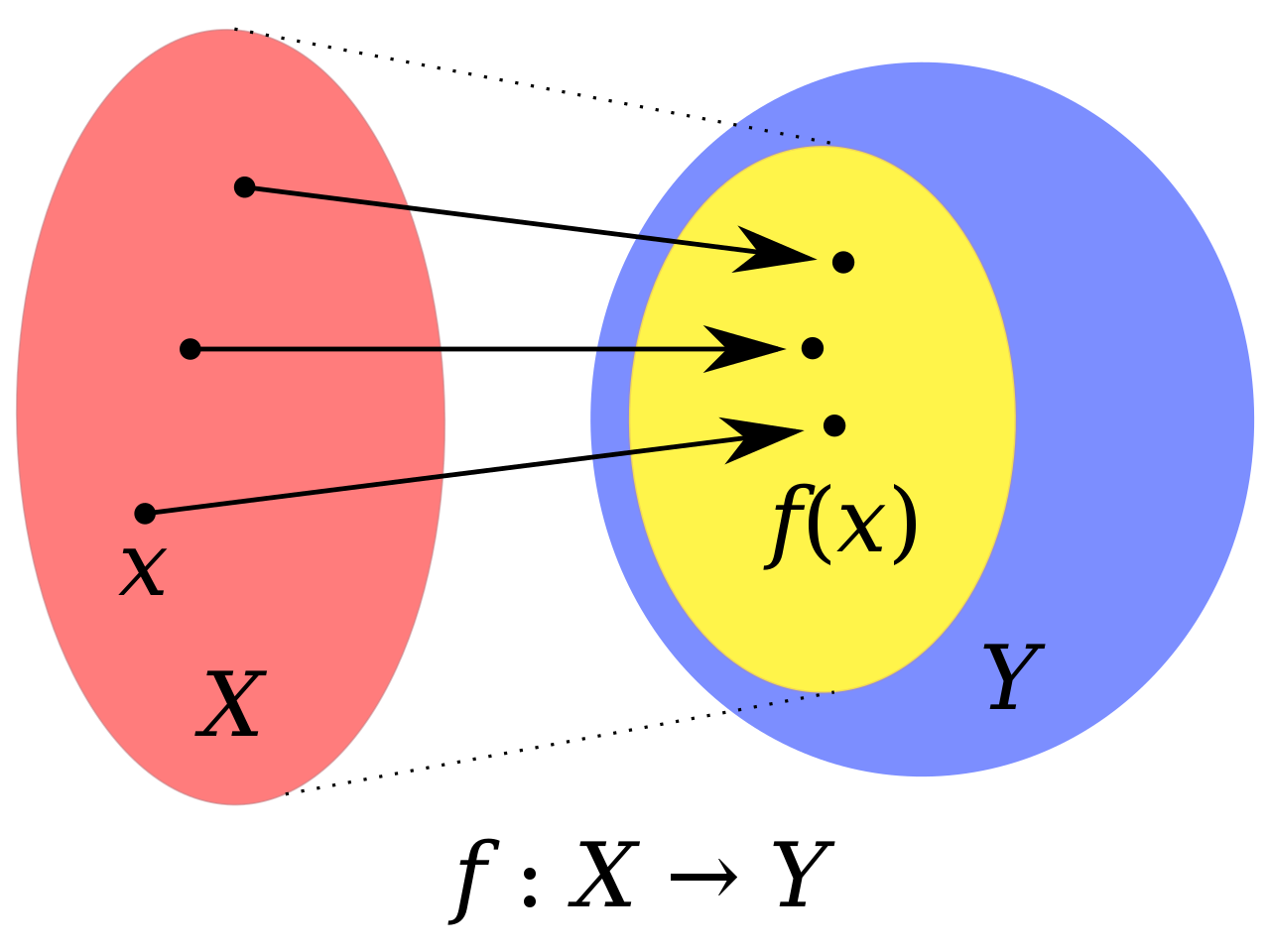
선형변환에서 말하는 정의역, 공역, 치역은 각각 어떤 것인가?

그것이 바로 4개의 부분공간(row space, null space, column space, left null space)이 의미하는 바이다.

---

3.벡터공간(vector space)이란?

벡터 공간(Vector Space)은 벡터들의 집합으로,

합(sub)과 스칼라 곱(scalar multiplication)의 연산을 정의할 수 읐으며,

그에 대한 8가지 조건을 만족해야 한다. 

---

4.부분공간(subspace)이란?

전체 집합과 부분 집합의 관계라고 생각하면 된다. 

즉, 벡터 공간의 부분집합이다.

 

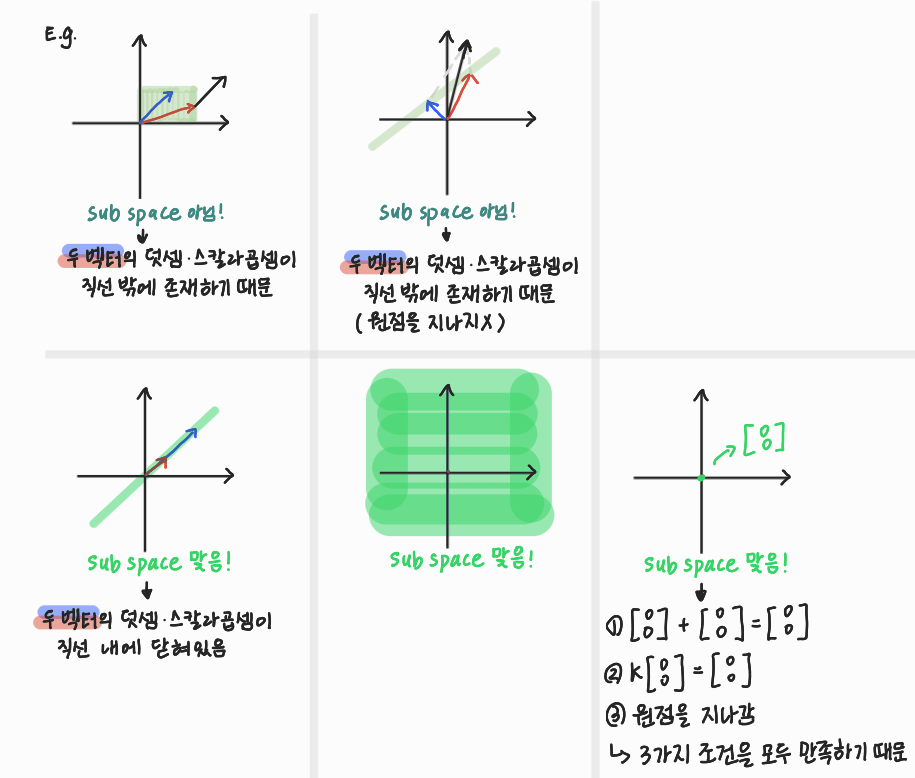
벡터 공간의 아무 부분집합이나 부분공간이 되지는 않는다. 

부분공간을 만족하기 위해서는 아래 3가지 조건을 만족시켜야 한다.

---

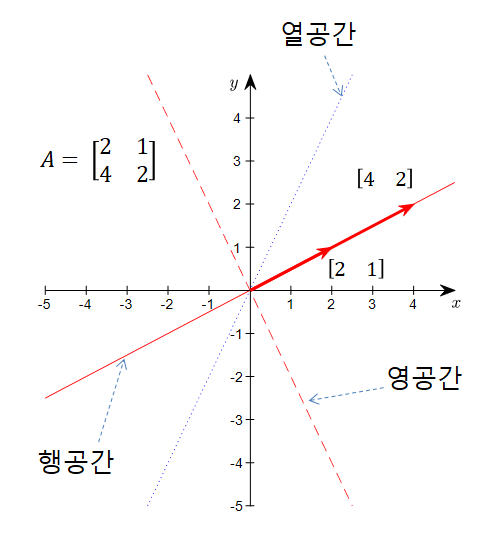
5. 행공간(row space)과 열공간(column space)

행렬 A의 모든 행(row) 혹은 모든 열(column)들의 선형결합으로 구성된 벡터공간은 '부분 공간'이며,

각각을 행공간(row space), 열공간(column space)이라고 부른다.

 

 

1) 행공간은 어떤 m x n 행렬의 행공간을 행 벡터로 span할 수 있는 \( [R]n \) 의 부분 공간이다.

따라서, 행공간의 벡터들은 n 개의 성분을 가지고 있다.

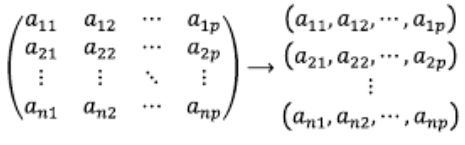
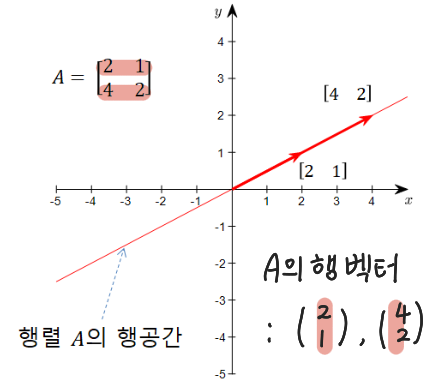
A의 행 벡터 = \(A^T \)의 열 벡터 

--> C( \(A^T \) ) = A의 행공간

 

E.g. 벡터 [2 1]와 [4 2]의 선형결합으로 이루어진 선 상에 있는 모든 벡터들의 집합이다.

 

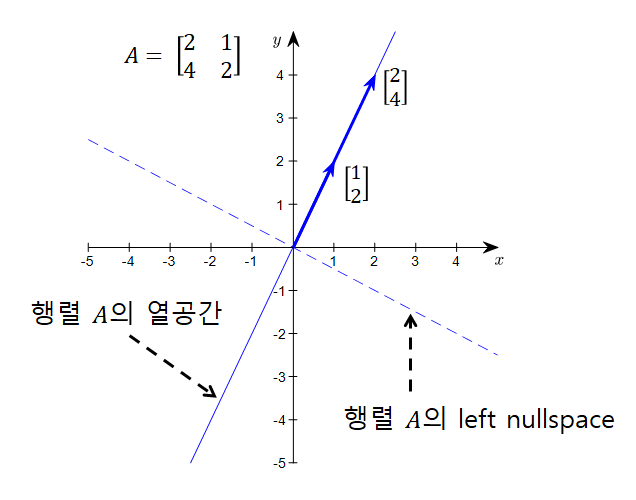
2) 열공간은 어떤 m x n 행렬의 행공간을 열 벡터로 span할 수 있는 \( [R]m \) 의 부분 공간이다.

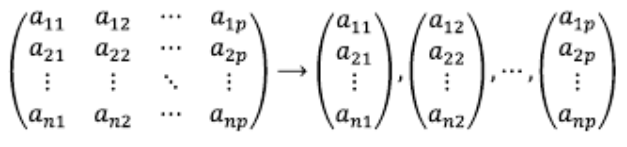
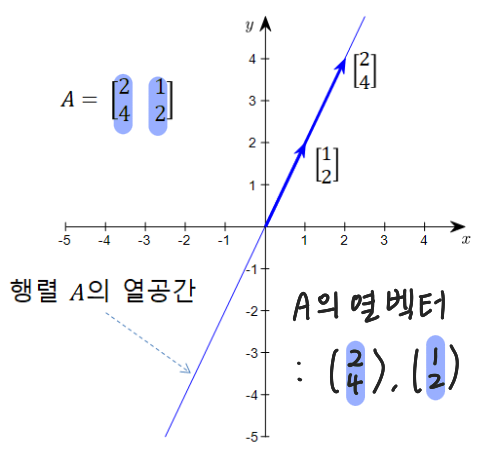
E.g. 벡터 \( [2 \quad 1]^T \)와 \([4 \quad 2]^T\)의 선형결합으로 이루어진 선 상에 있는 모든 벡터들의 집합이다.

---

6. 영공간(null space)

행렬 A에는 영공간(null space)이라는 부분 공간도 존재한다.

영공간은 아래와 같은 조건을 만족하는 \( \overrightarrow{x} \)들의 집합이다.

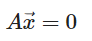
즉, 행렬 A가 주어질 때 A \( \overrightarrow{x} \)=0을 만족하는 모든 벡터 x들의 집합이다.

---

7.부분 공간(subspace)들간의 관계 

함수란 무엇인가?
함수 f의 정의역 X, 공역 Y, 치역 f(x)일 때,
함수는 정의역의 각 원소를 정확히 하나의 공역 원소에 대응시킨다.

 

m×n 차원의 행렬이라면 ,

선형변환에서 말하는 정의역, 공역, 치역은 각각 어떤 것인가?

• (입력)정의역 = n차원 벡터 공간 = row space + null space = \( [R]^n \) 
• 공역 = m차원 벡터 공간 = column space + left null space
• (출력)치역 
• 공역  - (출력)치역 = left null space  

즉, 만약에 A ∈ \( [R]^mxn \)  이라면 이 행렬은 다음과 같은 함수이다.

 

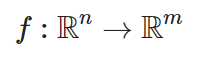
직교 관계 

(1) 행공간(row space)과 영공간(null space)의 관계

= 서로 직교하는 공간

= 내적값이 0이다

 

차원 = 기저 벡터의 개수

즉, 벡터 공간을 구성하는 데에 필요한 최소한의 벡터 개수다.

 

(2) 열공간(column space)과 영공간(left null space)의 관계

= 서로 직교하는 공간

= 내적값이 0이다

---

※ 개인공부 목적으로 정리한 내용들입니다.

출처

https://angeloyeo.github.io/2020/11/17/four_fundamental_subspaces.html#%ED%96%89%EB%A0%AC%EC%9D%80-%EC%84%A0%ED%98%95%EB%B3%80%ED%99%98%EC%9D%B4%EB%8B%A4

4개 주요 부분 공간의 관계 - 공돌이의 수학정리노트 (Angelo's Math Notes)

https://losskatsu.github.io/linear-algebra/linear-trans/#2-%EB%91%90-%EB%B2%A1%ED%84%B0-%EA%B3%B5%EA%B0%84-%EC%82%AC%EC%9D%B4%EC%9D%98-%ED%95%A8%EC%88%98

[선형대수] 선형변환(linear transformation)의 의미

https://mldlcvmjw.tistory.com/409

행 공간, 열 공간, 영 공간, 랭크, 널리티

https://portrait-of-youngblood.tistory.com/27

15. 벡터 공간 (Vector Space)

 

https://www.youtube.com/watch?v=0gHg5X6ng_4

https://www.youtube.com/watch?v=g0eaDeVRdZk&list=PL_iJu012NOxdZDxoGsYidMf2_bERIQaP0&index=8